
The observational nature of the study introduces a selection bias into the estimated average treatment effect as the lack of randomization can cause the treated and control groups to be different in terms of baseline characteristics (Lunceford and Davidian 2004). The present work is inspired by an observational study, where the objective was to explore the potential of oral anticoagulant treatment (OAT) in reducing the risk of mortality due to atrial fibrillation in patients with end-stage renal disease (ESRD) (Genovesi et al. Due to various reasons, including costs, ethicality, and the growing easiness of access to registers and large follow-up data, observational studies are increasingly used for the evaluation of treatment effect differences between groups of individuals (Austin 2019). When the goal is to establish the causal effects of treatments, randomized controlled trials (RCTs) are the gold standard (Kovesdy et al. Further, we showed that IPSW is still useful to account for the lack of treatment randomization, but its advantages are stringently linked to the satisfaction of ignorability, indicating that the existence of relevant though unmeasured or unused covariates can worsen the selection bias. Using extensive simulations, we show that BC-IPSW substantially reduced the bias due to the misspecification of the ignorability and overlap assumptions. The benefit of the treatment to enhance survival was demonstrated the suggested BC-IPSW method indicated a statistically significant reduction in mortality for patients receiving the treatment. The approach was motivated by a real observational study to explore the potential of anticoagulant treatment for reducing mortality in patients with end-stage renal disease. We present a bootstrap bias correction of IPSW (BC-IPSW) to improve the performance of propensity score in dealing with treatment selection bias in the presence of failure to the ignorability and overlap assumptions. However, IPSW requires strong assumptions whose misspecifications and strategies to correct the misspecifications were rarely studied. The inverse propensity score weight (IPSW) is often used to deal with such bias. When I did this, I got approximately -.21 for the ATT.When observational studies are used to establish the causal effects of treatments, the estimated effect is affected by treatment selection bias. You can do this many times and average them to get even closer to the true ATT. That should produce an estimate close to the true ATT. You can use simulations to estimate the ATT given that you know the parameters of the outcome-genertaing process: in a large dataset, compute the predictor means at A=1 (i.e., mean(x1), mean(x2), and mean((x1*x2))), and then plug those into the formula, i.e., -3 + 5*mean(x1) - 10*mean(x2) + 15*mean((x1*x2)) The unfortunate part is that there is in general no clear way to find the predictor means in the treated group analytically. To find the ATT, you would need to evaluate the combined coefficient on A at the predictor means in the treated group. (Note that the final term should include the mean of x1*x2, which in this case happens to be the product of the means of x1 and x2, but won't always). Which does equal -.775 as you have figured out. The formula for the ATE is the combined coefficient on the A when evaluating the predictors at their means, i.e., -3 + 5*.55 - 10*.3 + 15*(.55*.3) Sadly, there is no closed-form solution for the ATT except in certain cases. How would you find the expected ATT using the same data generating process formulas in the above example?
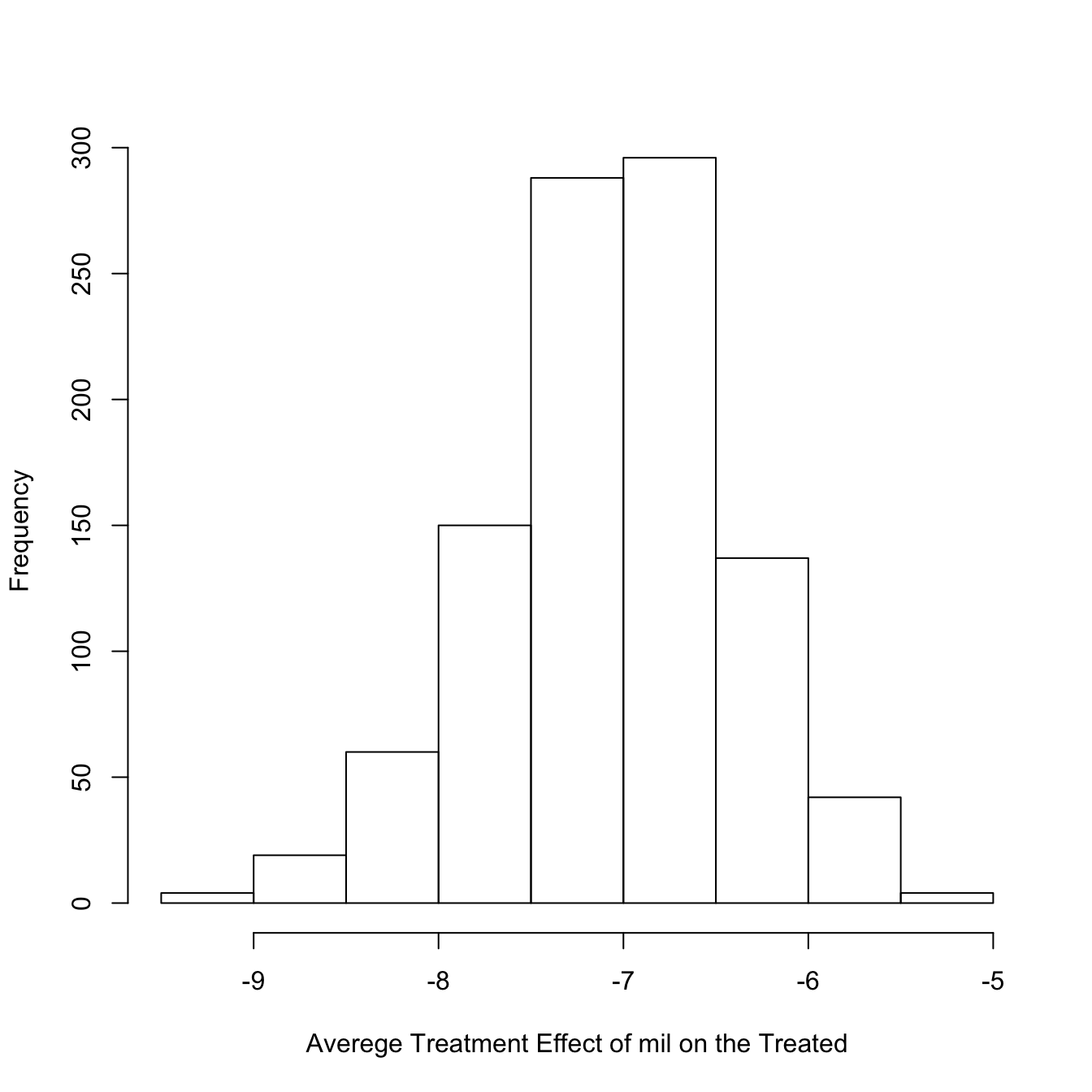
However, many techniques find the Average Treatment Effect on the Treated (ATT), not the ATE. # Expected ATE for Y = E(Y|A=1) - E(Y|A=0) # Observational Studies", Schuler & Rose, 2016 # This works great for the Average Treatment Effect (ATE) - you can directly compute the expected ATE from the data generating process in the following R code: # Simulation data from "Targeted Maximum Likelihood Estimation for Causal Inference in # I'm running comparisons of different counterfactual modeling methodologies (exact matching, propensity score matching, regression, etc.) on simulated data in order to see which methods produce the most precise estimates of the "true" population treatment effects.


 0 kommentar(er)
0 kommentar(er)
